|

У Миши 2 яблока, а у Маши в 3 раза больше. У Миши 5 рублей, а у Маши в 2 раза больше. У Миши 4 карандаша, а у Маши в 4 раза больше. Требуется найти, сколько яблок, денег, карнадашей у Маши.
Три задачки однотипные. Общий метод их решения таков: Мишины вещи умножаем на число раз и получаем Машины вещи.
Математики не любят словесных правил, они предпочитают изъясняться кратко, языком формул. Обозначим Мишины предметы буквой а, Машины буквой b, а разы буквой n. Тогда
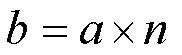
Такая формула будет универсальным средством для решения всех задач подобного типа. А зачем формула? И без нее все прекрасно решается. Конечно решается, но это ведь суперлегонькая задачка. А если что потруднее, к примеру хотя бы квадратное уранение с дискриминантами. Там без формул надо бы было всякий раз заново изобретать велосипед. А с формулой - милое дело! - один раз вывел, запомнил, и пользуйся сто лет, не задумываясь, откуда она взялась.
Когда мы заменяем числа буквами - тут кончается арифметика и начинается алгебра. Алгебра позволяет выявлять общие правила действия над числами и облегчает вычисления.
Буквы, числа и знаки арифметических действий, записанные рядышком, называются АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. Например, вот это - разные алгебраические выражения:
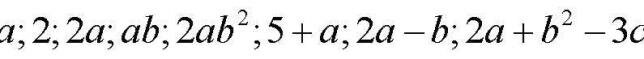
Алгебраические выражения бывают двух разновидностей - ОДНОЧЛЕНЫ и МНОГОЧЛЕНЫ. В приведенном примере
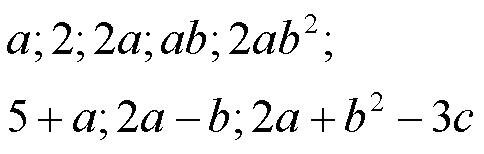
первая строчка - это пять одночленов, вторая строчка - это три многочлена. То есть, одночлен - это или одна буква, или одно число, или буквы и числа, связанные действиями умножения, деления, возведения в степень, извлечения корня.
А если два или больше одночленов связываются знаками плюс или минус - получаются многочлены. Многочлены, в свою очередь, бывают такие:ДВУЧЛЕНЫ, ТРЕХЧЛЕНЫ и дальше просто МНОГОЧЛЕНЫ. Иногда говорят на латыни: БИНОМЫ, ТРИНОМЫ, ПОЛИНОМЫ.
Умножение и сложение одночленов
Умножать одночлены очень легко
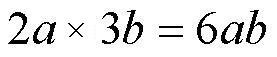
То есть числовые коэффициенты перед буквами перемножаются, а буквы прямо так и записываются. Заметим, что в арифметике мы всегда писали знак "умножить", или такой 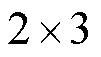 или такой или такой 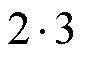 Если в арифметике знак не поставить, то это будет уже не действие, а просто двухзначное число 23. А в алгебре с буквами знак "умножить" не ставится, а подразумевается. Не пишут вообще ни в каком виде! Если в арифметике знак не поставить, то это будет уже не действие, а просто двухзначное число 23. А в алгебре с буквами знак "умножить" не ставится, а подразумевается. Не пишут вообще ни в каком виде!
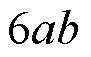 означает то же самое, что означает то же самое, что 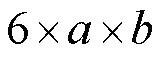
Если умножение такое 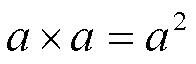 мы знаем, что число, умноженное само на себя два раза - это число "в квадрате", вторая степень; если три раза - "в кубе", третья степень, пять раз - в пятой степени и так далее. мы знаем, что число, умноженное само на себя два раза - это число "в квадрате", вторая степень; если три раза - "в кубе", третья степень, пять раз - в пятой степени и так далее.
СЛОЖЕНИЕ. Складывать одночлены легко, если они ПОДОБНЫЕ. Подобными называются такие, которые отличаются друг от дружки только числовым коэффициентом. Например, подобные одночлены
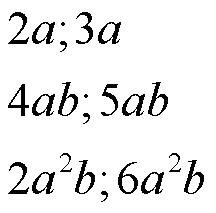
При сложении получится
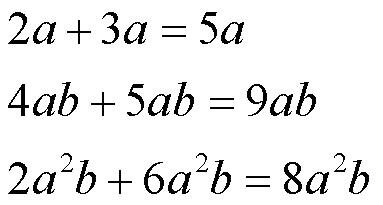
То есть, правило легкое - складываем (или вычитаем) только числовые коэффициенты, а буквы оставляем, как были. Это действие часто называют ПРИВЕДЕНИЕМ ПОДОБНЫХ ЧЛЕНОВ. Если складывать НЕподобные члены - то получится многочлен.
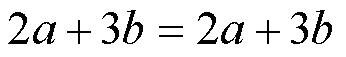
Так вот и получится, по отдельности, у НЕ подобных ни числовые коэффициенты, ни буквы складывать между собой нельзя.
Сложение и вычитание многочленов
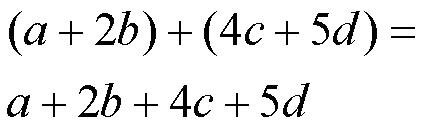
Вот так, тупо убираем скобки и все! А если вычитание, тогда
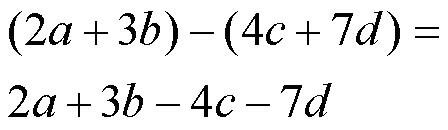
То есть, если перед скобкой стоял знак минус, то не просто тупо убираем скобки, а знаки всех одночленов, стоявших внутри этих скобок, меняем на ПРОТИВОПОЛОЖНЫЕ (плюс на минус, минус на плюс)
Третий пример
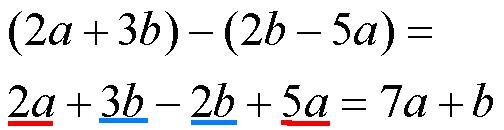
Здесь после отбрасывания скобок (или говорят РАСКРЫТИЯ СКОБОК) образовались две пары подобных членов, они подчеркнуты красным и синим цветом, мы их ПРИВЕЛИ и получили 7a и 1b. Но единичку перед буквой писать не принято, ее мы просто подразумеваем, поэтому получилась просто b.
Умножение одночлена на многочлен
Это делается так
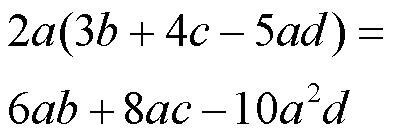
Правило тут такое: одночлен, который стоит перед скобкой, последовательно умножают на каждый член многочлена. Само собой, соблюдаем знаки: плюс на минус или минус на плюс - будет в итоге минус. А плюс на плюс или минус на минус - будет плюс.
Умножение многочлена на многочлен
Это несколько трудоемко, и на первый взгляд может показаться громоздким, но на самом деле - весьма просто. Каждый член одного многочлена последовательно умножают на каждый член второго многочлена.
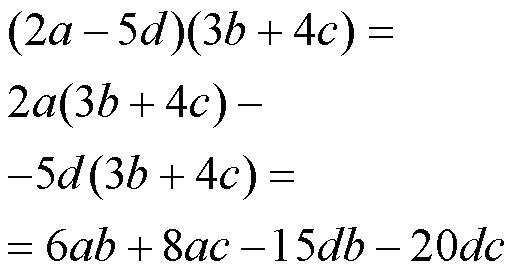
Когда стоят две буквы рядом (в смысле умножаются друг на друга) их принято таки писать в алфавитном порядке, то бишь красивше писать не 20dc, а 20cd. Хотя с точки зрения математики это не важно, от перемены мест произведение не меняется и ответ не испортится.
Формулы сокращенного умножения
Некоторые особенные сочетания многочленов встречаются чаще остальных. Поэтому их запоминают и потом используют по памяти. Например, так называемая разность квадратов
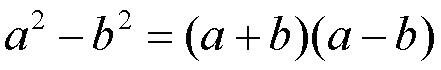
То, что эта формула справедлива, очень легко доказать. Надо сделать умножение многочлена на многочлен, а потом привести подобные члены. Проверим:
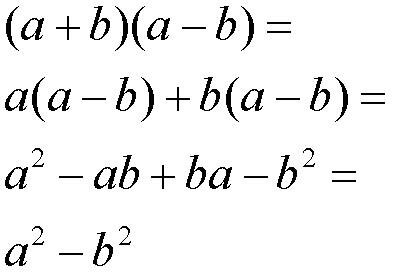
Здесь ab и ba -это одинаковые одночлены, от перемены мест не меняется, но они с противоположными знаками. Поэтому при сложении они дают в результате нуль (говорят - ВЗАИМНО УНИЧТОЖАЮТСЯ) и остаются только квадраты двух a и b.
В школе нас заставляли учить КВАДРАТ СУММЫ, КВАДРАТ РАЗНОСТИ, КУБ СУММЫ, КУБ РАЗНОСТИ и даже БИНОМ НЬЮТОНА. Кто их выучил - хорошо, конечно, но так уж сильно их учить не надо. Всегда можно вывести простым перемножением многочленов. Например
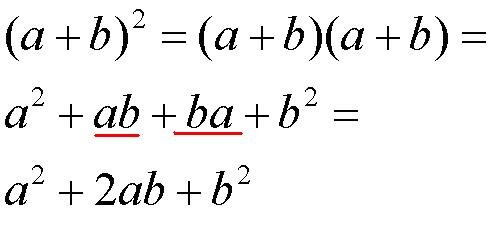
Скобка "в квадрате" - это значит скобка умножается сама на себя 2 раза, перемножаем, потом приводим подобные члены, они подчеркнуты красным цветом, вот и получаем что надо. Если квадрат разности - там знаки будут другие. Если куб, то есть третья степень - надо перемножать три одинаковых скобки. Это делают так. Сначала перемножают два многочлена, приводят все подобные члены и в результате получают новый многочлен; а потом уж третью скобку умножают на этот многочлен. В общем, если попадется, разберетесь....
В начало страницы
|
|
![]()

