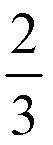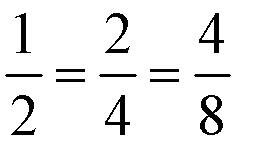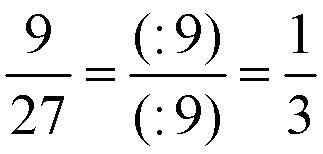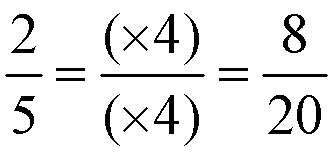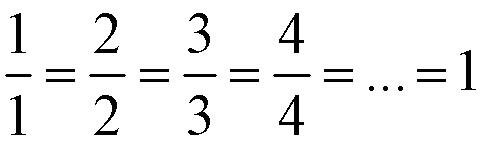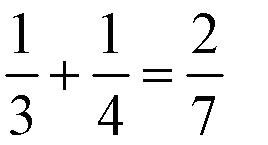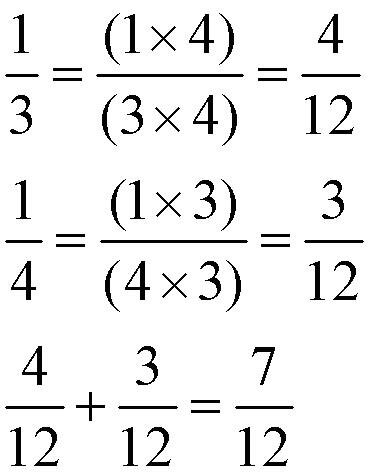Задачка: два яблока разделить поровну между тремя мальчиками. Очевидно, надо поступить так: каждое яблоко разрезать на 3 равных части, получится 6 частей, и каждому мальчику дать по 2 получившихся кусочка. Сколько получит один мальчик? Он получит меньше, чем целое яблоко, он получит два кусочка, а каждый кусочек - это треть (третья часть) целого яблока. Мальчик получит ДВЕ ТРЕТИ. В математике принято писать так:

Число снизу под дробной чертой, оно называется ЗНАМЕНАТЕЛЬ ДРОБИ, показывает, на сколько частей было разрезано яблоко. Число сверху - ЧИСЛИТЕЛЬ ДРОБИ -показывает сколько кусочков получил мальчик.

Хотя, воможно и такое деление...

Кстати, ха-ха, вспомнилась еще одна задачка с приколом. В корзине лежат три яблока. Как разделить их между тремя мальчиками, чтобы каждый получил по ЦЕЛОМУ числу яблок, а одно яблоко осталось в корзине?
Но это так, не совсем по теме. Дробь еще удобно представлять в виде разрезанных кружочков, типа порезанного тортика.

Воображая разные комбинации кусоков торта, мы придем к выводу, что

То бишь, если торт разрезать на две части и взять одну из них - это ПОЛОВИНА торта. Если разрезать на 4 части и взять две из них - это тоже ПОЛОВИНА торта. Если разрезать на 8 частей и взять 4 из них - тоже ПОЛОВИНА торта. Из этих "манипуляций" вытекает ОСНОВНОЕ СВОЙСТВО ДРОБИ:

Дробь не изменится, если и числитель, и знаменатель одновременно умножить или разделить на какое-нибудь число

Это свойство применяют, когда сокращают дробь (делают поменьше и числитель и знаменатель), например

Но можно, если это зачем-нибудь понадобится, и наоборот увеличить числитель и знаменатель:

Еще бы хотелось отметить такое, понятное ежику, свойство

Дробь, у которой числитель и знаменатель одинаковые, равна 1 (единице).

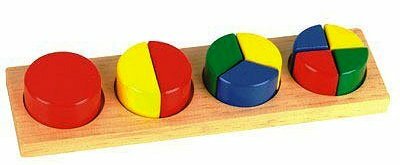
На картиночке одна целая, две вторых, три третьих, четыре четвертых

Сложение и вычитание дробей

Понятно, что 1/3 яблока плюс 1/3 яблока будет 2/3 яблока. То есть дроби с одинаковыми знаменателями складываются и вычитаются легче легкого.
А как сложить, например 1/3 и 1/4? Это же не одинаковые кусочки яблока?
Какой-нибудь тупой дебил сделал бы так:

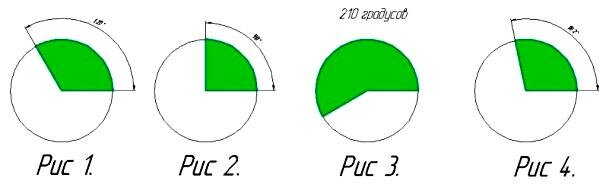
Это НЕПРАВИЛЬНО! НЕПРАВИЛЬНО! Смотрите, почему. Вот кусочек торта (рис 1), соответствующий дроби 1/3. Его ограничивает центральный тупой угол величиной 120 градусов.

Вот кусочек тортра 1/4 (рис.2). Его ограничивает центральный прямой угол величиной 90 градусов.Если бы мы сложили вместе эти два кусочка, то получился бы кусман с углом 120+90=210 градусов, такой, как на рисунке 3. А тупой дебил получил кусочек 2/7, то есть с углом 102 градуса (рис.4), чуть не в два раза меньше, чем правильный кусок. Так ему за тупость и надо!

А как же поступим мы - умные люди? А так. Мы скажем твердо и уверенно: СКЛАДЫВАТЬ МОЖНО ТОЛЬКО ДРОБИ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ. Если даны с неодинаковыми - надо сначала сделать их с одинаковыми, используя основное свойство дроби, а уж потом складывать.

Видите, в первой дроби мы и числитель, и знаменатель одновременно умножили на 4; а во второй на 3. Получили две дроби с одинаковым знаменателем 12, которые потом легко и просто сложили!
А откуда мы взяли, что нужно первую дробь умножать на 4, вторую на 3, а знаменатель одинаковый должен быть равен 12? Это мы прикинули в уме. Если "прикидывалка ума" не очень хорошо работает - можно знаменатели перемножить; 3 умножить на 4 будет 12, а потом поглядеть, на сколько надо домножить каждую дробь, чтобы подогнать ее к общему знаменателю.
Это действие - преобразование дробей так, чтобы знаменатели были одинаковыми - называется ПРИВЕДЕНИЕ К ОБЩЕМУ ЗНАМЕНАТЕЛЮ. А после того как привели - общий знаменатель пишут под общей дробной чертой, а над чертой складывают числители. Вот это правильно! Посмотрите-ка видео для закрепления.

Умножение и деление дробей

А теперь, прикиньте, тупому дебилу задали решить пример:

Он, как вы поняли, сделал вот так:

И, что удивительно - он оказался прав! Так и делается умножение дробей! Неисправные часы тоже два раза в сутки показывают правильное время. Тупой дебил, глядишь, да и попадет в яблочко "методом слепого тыка".

Деление чуть-чуть похитрее:

Для деления сначала надо одну дробь (без разницы какую, хоть первую, хоть вторую) надо перевернуть кверх ногами, то есть числитель поставить на место знаменателя, а знаменатель на место числителя, а потом выполнить обыкновенное умножение.

Десятичные дроби

Десятичные дроби - это дроби со знаменателем 10, или 100, или 1000, или любое другое число, кратное десятке. Их можно записывать так же, как обыкновенные:

Но придумана и другая форма записи:

Впереди нулик, он указывает, что целых нет, дробь меньше единицы. Потом первый знак после запятой, указывает, сколько десятых; второй - сколько сотых; третий - сколько тысячных и так далее...
Чем же хороши десятичные дроби? Отчего нам не хватило обыкновенных и мы придумали еще и десятичные?
Во-первых, из-за того, что у нас на руках десять пальцев и мы любим все считать десятками, сотнями, тысячами. У нас и деньги такие. Нет купюр достоинством 60 рублей, или 120 рублей, но зато есть 10 руб., 100 руб., 1000 руб. Те же проценты, которые мы рассматривали в задаче В1, это 1/100 часть числа, или в десятичной форме записи 0,01.
А во-вторых, складывать десятичные дроби намного легче, чем обыкновенные. Надо их записать в столбик и сложить по разрядам, как мы поступаем при сложении многозначных чисел.

Не надо тебе никаких общих знаменателей и прочей дребедени. Только помните - надо записывать ровно: запятая под запятой, разряд под разрядом.
Так же, как многозначные числа умножают и делят десятичные дроби.

Чуть не забыл! А как там с яблоками из корзины? Ответ такой: каждому пацику надо, конечно, дать по целому яблоку, но одному - вместе с корзиной.

В начало страницы