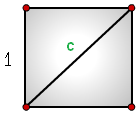
Натуральные числа

Давным-давно, на заре цивилизации появились так называемые НАТУРАЛЬНЫЕ ЧИСЛА. От слова «натура» - природа. Это такие числа, с помощью которых можно считать предметы. А именно: 1, 2, 3, 4, 5, 6 и так далее. Дело, я думаю, было так. Мужики первобытного племени отправляются на охоту. Хорошо, если повезет и завалят мамонта. А если мамонта не встретишь, и придётся охотиться на мелкую дичь, каких-нибудь куропаток или сусликов. Тогда охотиться придется до тех пор, пока не настреляешь по одной куропатке на каждого члена племени. А то ребята не насытятся, да ещё и раздерутся. Следовательно, надо до начала охоты пересчитать потенциальных едоков, а после охоты пересчитать добычу. И сопоставить, чтобы эти числа были равны.

Вот и придумали люди натуральные числа. Вероятно, они пользовались для счета пальцами, когда пальцы кончались – они откладывали для памяти камешек и начинали счет следующего десятка опять с первого пальца. Так возникла ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. Если бы у древних мужиков было бы не по пять, а по четыре пальца – система счета была бы другая.

Какое самое маленькое натуральное число? Конечно, 1. Ибо самое малое число предметов – один, меньше штук предметов не бывает. А самое большое какое? А самого большого не бывает. Если бы было какое-то число самое большое – мы бы прибавили к нему 1  и получили бы больше, чем самое большое. Говорят, что натуральный ряд чисел бесконечен. Если какое то число  a натуральное, то иногда пишут так

(«a принадлежит N»). Этот вот значок, похожий на паучка, тянущего лапки в одну сторону, означает ПРИНАДЛЕЖИТ.
А буквой N обозначают в данном случае множество всех натуральных чисел.

Целые числа

Натуральные  числа понятны, очевидны, их можно потрогать в буквальном смысле. Но - увы! – их мало, чтобы описать окружающий мир. Ведь в натуральном ряде есть начало и нет конца. А у многих  явлений природы нет ни конца, ни начала.
Например, время. Наш вселенная в каком-то виде существовала бесконечное множество лет назад и будет существовать бесконечно в будущем. Возможны катаклизмы, разрушения планет и угасание звезд, но в целом материя вечна. А как же отсчитывать время? Как отыскать начало всех времен?
А его и не ищут. Мы берем некий условный момент – рождество Иисуса Христа – и считаем его за начало времен:
00 часов, 00 минут, 00 секунд самого первого года. И  от этого начала отсчитываем в две стороны – «наша эра» и «до нашей эры».
Примерно так же поступают и с температурой. Возможны «бесконечная жарища» и «бесконечный холодище»; от чего же начинать отсчет? Договорились принять за нуль температуру таяния льда. Все, что холоднее – ниже нуля; все, что теплее – выше нуля.
(Заметим в скобках: позднее доказали, что «бесконечного холодищи» не бывает. Есть абсолютный нуль (минус 273 градуса по Цельсию), ниже которого невозможно охладить никакое тело).
Так же поступаем и с числами. Возьмем некоторую прямую, разделим ее на равные деления, например по сантиметру.
Какую то любую (от балды!) точку будем считать началом отсчета и обозначим числом 0. Вправо от нее пойдут положительные числа, влево – отрицательные.

Положительные числа можно писать со знаком +, но можно не писать, а только подразумевать. Отрицательные числа всегда пишут со знаком -. Ясно, что такая прямая бесконечно простирается в обе стороны, иногда пишут

(от минус бесконечности до плюс бесконечности). Положительное направление обозначают стрелкой. Таким вот манером размаркированная линия называется ЧИСЛОВАЯ ОСЬ.

Натуральные числа вот еще чем плохи. Действие сложения, типа

12 + 5 = 17

в них всегда выполнимо. А действие вычитания выполнимо не всегда. Например действие

12 - 5 = 7

выполняется, а действие

5 -12 =?

пользуясь только натуральными числами, выполнить нельзя. Добавив отрицательные числа и нуль, мы устраняем этот недостаток.
Сложение и вычитание легко производить, шагая по числовой оси. Например

2 + 4 =?

Мы должны встать на 2, а потом сделать 4 шага в положительном направлении (вправо, по стрелке). Очутимся где? На 6. Таким образом,

2 + 4 = 6

Чтобы сделать вычитание, мы должны шагать в обратном направлении (влево). Например

4 - 2 = 2

А если шагнуть так?

5 - 5 = ?

Мы очутимся на нуле, 5 - 5 = 0.

А если так?

6 - 8 = ?

Двинувшись влево, мы перейдем за нуль и очутися на - 2 (минус 2).

6 - 8 = - 2

Это правило "шагания" рекомендую усвоить, чтобы научиться выполнять действия с отрицательными числами.
Подытожим: Все целые положительные чила, все целые отрицательные числа и число нуль вместе составляют множество целых чисел.

Рациональные числа

Однако, этих чисел все еще недостаточно для жизни. Пользуясь только целыми числами всегда можно выполнить действие умножения, но не всегда выполнимо деление:

6 : 2 = 3

но 5 : 2 = ?

Поэтому добавляем еще числа дробные, кратко говорят ДРОБИ. Дроби бывают обыкновенные, типа ; бывают десятичные, типа 2,5 (о них мы подробнее поговорим во второй лекции); но по-любому ДРОБЬ - это не целое число, а целое с "хвостиком"; это больше, чем одно целое, но меньше, чем следующее за ним целое.
Само собой, дробные числа, дроби, могут быть как положительными, так и отрицательными.

И все вместе: положительные (целые и дробные), отрицательные (целые и дробные) и нуль - составляют множество рациональных чисел.

Действительные числа

Теперь-то нормалек? Все действия выполнимы? Все явления природы можно выразить?
Увы, нет! Есть еще одна штука, над которой ломали голову древние греки, а Пифагор из-за нее проклял арифметику и решил заниматься только геометрией, чтобы не было никаких чисел.
Это - вот какая штука. Во-первых, согласимся, что любой отрезок (например, начерченный на бумаге) имеет конечную длину и его можно измерить. А возьмем диагональ квадрата со стороной равной 1.

,

Согласно теореме Пифагора она равна

Если станем извлекать корень их двух - получим бесконечную непериодическую дробь.С бесконечным числом знаков после запятой! Конечно, для практических нужд мы можем оставить 2-3 знака, остальные отбросить и вполне удовлетвориться. Но в теории? Как так: объект есть, его длина вполне определенна и конечна, а такого числа, чтобы выразить длину объекта - нет? Можно записать

но все это будут лишь приближенне значения, округленные до скольких-то знаков после запятой. Точнее записать нельзя.
Такая, блин, у нас система счисления, что число это, вроде как, в природе есть (диагональ квадрата), а выразить его нельзя!
Такие числа незывают ИРРАЦИОНАЛЬНЫМИ ( то есть НЕ рациональными). К ним тоносятся, например

Их обычно так и пишут, как бы не выполняя действие извлечения корня, или условной буквой. Но всякий раз, когда мы пишем "пи", мы обязаны помнить, что это не просто какая-нибудь буква, типа a или x, а число примерно равное 3, а поточнее 3,14, а еще точнее 3,14158; но до конца с абсолютной точностью его записать невозможно.
РАЦИОНАЛЬНЫЕ + ИРРАЦИОНАЛЬНЫЕ числа вместе составляют МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ.

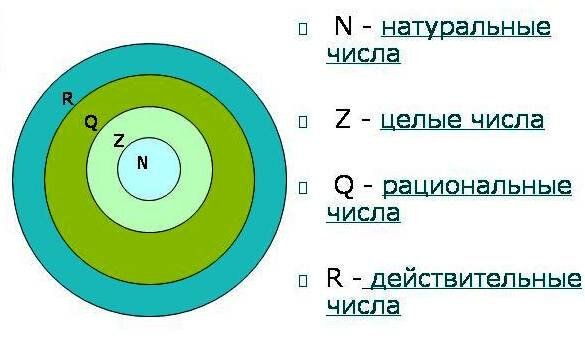
На картинке указано, какой буквой принято обозначать каждое множество, а круглая схема поясняет, что каждое предыдущее множество входит в состав следующего, более обширного.
Это все! Кроме действительных чисел есть еще так называемые МНИМЫЕ, но в школе их не проходят, и в ЕГЭ не сдают.

В начало страницы