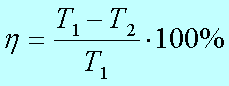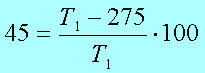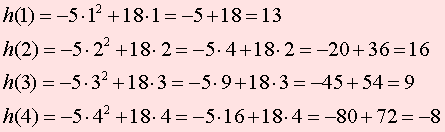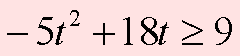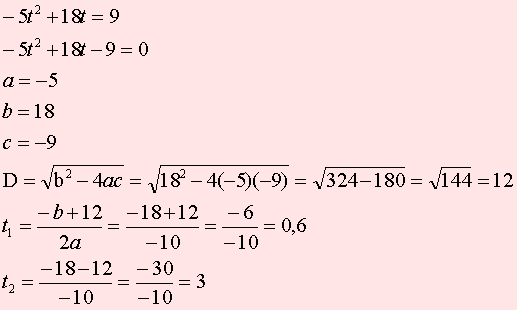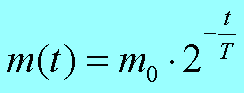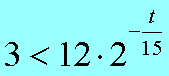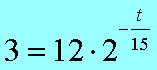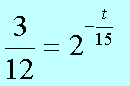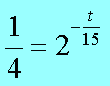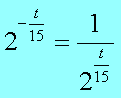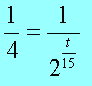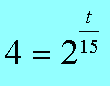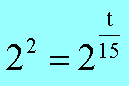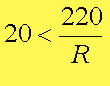Пример В12 – 1

Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой

Где Т1 –температура нагревателя в градусах Кельвина, Т2 – температура холодильника в градусах Кельвина.
При какой температуре нагревателя Т1 КПД будет 45% , если Т2 = 275 К? Ответ выразите в градусах Кельвина.

Решение. Задачки В12 сильно напоминают задачки по физике и этим некоторых напрягают. В общем-то не худо бы воображать описанный в задачке процесс, но и без этого воображения задачку вполне себе можно решить.
По сути дела, в формуле три буквы Т1, Т2 и «ню». Две из них известны, а третья Т1 неизвестна. В общем-то это просто-напросто уравнение, только записано в хитрой форме. Чтобы получилось нормальное уравнение, можно сразу известные буквы заменить числами

А теперь решаем это уравнение обычным способом.
1. Чтобы избавиться от дроби в правой части обе части уравнения умножаем на Т1.

2. Раскрываем скобки в правой части уравнения

3. Переносим члены, содержащие неизвестную величину, в левую часть

4. Выносим Т1 за скобки

Из последнего выражения легко находим Т1 = - 27 500/ - 55 = 500
Ответ: 500

Пример В12 – 2

Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой

где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров?

Решение. Вообще эту задачу можно попробовать решить тупо, если подставлять значения t = 1,2,3,4 и т.д. То есть определять, на какой высоте камень был через 1 секунду после броска, через 2 секунды, через 3 секунды, через 4 секунды и так далее.
Попробуем так решить:

Хорошо видно, что через 1 секунду камень был на высоте 13 метров, через 2 секунды – на высоте 16 метров, через 3 – на высоте 9 метров (начал уже падать), а через 4 – на высоте минус 8 метров (типа провалился уже ниже земли). Моно ли сказать, что ТРИ секунды камень находился или на высоте 9 метров или выше (но не ниже)?  Нет, не три, - скажет внимательный читатель. В течение первой секунды, пока камень взлетал, он какое-то время летел, пока не достиг высоты 9 метров. Такой метод решения не годится.
Ну, не годится - так не годится. Зато перебором вариантов мы получше въехали в тему задачки. Будем решать, как полагается – с помощью неравенства.
Поскольку высота по условию должна быть не меньше 9 метров, можно записать такое неравенство

Неравенство мы обычно решаем так. Сначала вместо знака «не меньше» пишем знак «равно» и решаем уравнение. Потом анализируем полученные корни – с какой стороны от них неравенство выполняется. У нас здесь получается квадратное уравнение, будем решать его по формулам квадратного уравнения, с помощью дискриминанта.

Вот что получилось. Через 0,6 секунд после броска камень, взлетая вверх,  пересек границу высоты 9 метров, и через 3 секунды, уже падая, он опять пересек эту границу. Получается, что выше 9 метров (или ровно на 9-ти метрах)  камень находился 3 - 0,6 = 2,4 секунды.
Ответ: 2,4

Пример В12-3

Масса радиоактивного вещества уменьшается по закону

В лаборатории получили вещество, содержащее в начальный момент времени m0 = 12 мг изотопа натрия-24, период полураспада которого Т  = 15 часов. В течение скольких часов содержание натрия-24 в веществе будет превосходить 3 мг?

Решение. Для упрощения заменим числами известные величины, а заодно и знак «равно» заменим на знак «больше»

Получили показательное неравенство (с переменной величиной t в показателе степени). Надо его решить, блин!
Как будем решать?
1. Сначала из неравенства сделаем уравнение.

2. Разделим обе части уравнения на 12 и сократим.

3. Вспомним  свойство степеней. Если число в отрицательной степени, то можно его записать в виде дроби, у которой в числителе 1, а в знаменателе это число в такой же, но положительной   степени. То есть

Тогда получится такое шикарное выражение

Между двумя частями уравнения знак равно, числители одинаковые, значит и знаменатели тоже будут равны

А 4 – это два в квадрате, то есть

Основания степеней равны, значит равны и показатели

Ответ: 30

Пример В12-4

Решение. Здесь, конечно, без мало-мальского понимания физики можно затупить. Сила тока обозначается буквой I.  Из формулы (это формула закона Ома для участка цепи) видно, что сила тока зависит от двух параметров: от напряжения U и от сопротивления R.  Напряжение задано в исходных данных, оно равно 220 Вольт, никакой свободы выбора для нас нет. А сопротивления можно подбирать. Если к примеру сопротивление R = 100 Ом. Тогда ток будет 220/100 = 2,2 Ампера. В условии сказано, что в цепь включен предохранитель, рассчитанный на максимальный ток 20 Ампер. Как только ток в цепи станет равен 20 Ампер, предохранитель перегорит и отключит цепь. Пока у нас 2,2 ампера, это намного меньше, чем 20, цепь продолжает работать.
А пусть возьмём R=50 Ом. Тогда сила тока будет равна 220/50= 4,4 Ампера, тоже ничего, цепь продолжает работать.
Таким образом, при уменьшении сопротивления сила тока увеличивается, и требуется найти такое самое маленькое значение сопротивления, при котором сила тока не превысит 20 Ампер.
Иначе говоря, в переводе на язык математики, надо решит такое неравенство

Оно решается довольно просто. Сначала решаем уравнение 20= 220/R
Находим R =220/20 = 11. Потом анализируем. При R>11, I<20. При R<11, I>20.
Ответ:11
(Кстати говоря, в пособии Семенова приведен неправильный ответ на эту задачу)

Вот ролик по заданию в12 из ЕГЭ 2012 года, посмотрите, если хотите

Назад к задаче В11 /Задача В12/ Вперед к задаче В13