Задачка № А6 - про механические колебания. Давайте начнем опять с теоретической подкладки. КОЛЕБАНИЯ. Рассмотрим маятник:
И абстрактный грузик на веревочке, и весёлую девочку на качелях мы будем считать маятником. И тот, и та совершают повторяющиеся (периодические) движения, которые мы называем КОЛЕБАНИЯМИ. Колебания характеризуют двумя параметрами: ПЕРИОДОМ и АМПЛИТУДОЙ. Амплитуда - это "размах". Причем, размах не от края до края, а наибольшее отклонение от положения равновесия в любую сторону.А период? Это время, за которое маятник совершает одно полное колебание. Вот он начал движение из крайней правой точки. Мы включили секундомер. Он качнулся влево и снова вернулся в ту же точку, откуда стартовал. Мы выключили секундомер. Это время - и есть один период колебаний маятника. Вот на эту тему задачка из Демо-2014
Математический маятник - это грузик, не имеющий размеров (материальная точка), подвешан на нерастяжимой нити, и колеблется он в безвоздушном пространстве. То есть, такой чисто умозрительный условный объект. Как изменяется его потенциальная и кинетическая энергия при колебаниях - об этом мы весьма подробно рассуждали при разборе задачи А5. Если он начал движение с крайней правой точки (чёрной), то потенциальная энергия достигнет максимума в крайней левой точке. Это произойдёт через полпериода. Верный ответ №3. Другие задания демоварианта 2014 года смотри ЗДЕСЬ Кстати говоря, есть интереснейший вопрос. От чего зависит период колебаний маятника? Почему один маятник раскачивается солидно и неторопливо, а другой мельтешит туда-сюда? Может быть, период зависит от массы маятника? Может быть от амплитуды? Ответ довольно неожиданный - ТОЛЬКО ОТ ДЛИНЫ НИТИ ПОДВЕСА. Ну, и от ускорения свободного падения, которое всегда одинаковое.
Не зря маятники используют для часов. Период их колебания - ровно секунда. Если часы отстают или спешат - длину маятника маленько добавляют или укорачивают. Имейте это в виду. Посмотрим еще одну задачку, из демоварианта 2013 года. Она на понятие "амплитуда".
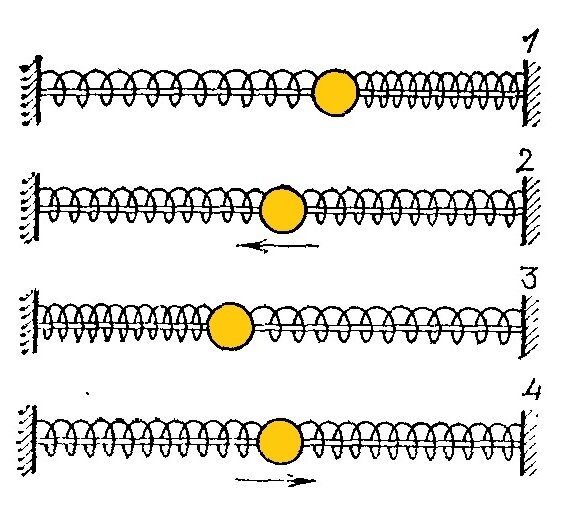
Здесь, как видите, колебания не маятника, а некого грузика на пружинках вдоль горизонтальной оси. Например, такого
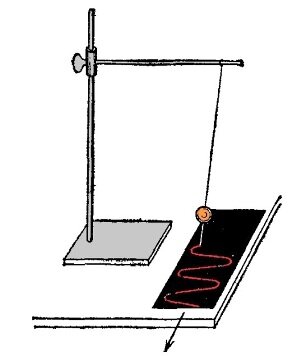
Но ничего принципиально не меняется. И для такого колебательного движения есть период и амплитуда. По таблице видим, что в одну сторону ( в плюс) грузик отклоняется на 15 мм, а в другую на минус 15. Это и есть амплитуда - наибольшее отклонение от положения равновесия.Правильный ответ №3. Если к качающемуся маятнику приделать какой-нибудь карандашик, а под ним протягивать бумажную ленту с постоянной скоростью - то получим развертку колебаний во времени.
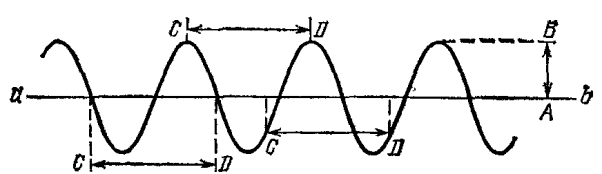
Развертка имеет такой вид:
Здесь АВ - это амплитуда - наибольшее отклонение маятника от положения равновесия. Её можно мерить хоть вверх, как на рисунке, хоть вниз. СD - это период, в данном случае расстояние, на которое протянули ленту за одно полное колебание маятника. CD - самая левая - это время от одного среднего положения маятника до другого среднего положения. CD - вторая(вверху) - это время от одного крайнего положения до другого крайнего. CD - самая правая - это период между некими промежуточными положениями, когда маятник находился в той же самой ФАЗЕ. Эта развертка очень похожа на синусоиду - функцию y = sinx, которую мы проходили по алгебре. Это и есть синусоида.Когда мы разбирали движение тела, мы там приводили функцию, которая показывает, где конктетно находится тело в данный (лпределённый) момент времени. Так вот, можно привести такую эе формулу и для колебания. Которая показывает, где конкретно находится маятник в данный момент времени. Формулы такие
Рассмотрим задачку из пособия Грибова, и по ходу её рассмотрения поясним значение входящих в формулу величин.
Ну, эта задачка просто на понимание формулы. Итак, в формуле буквой А обозначена амплитуда колебаний - наибольшее отклонение маятника от положения равновесия (в любую сторону). Буквой b (а по-хорошему буквой омега) обозначается частота колебаний. Частота обратна периоду. Период показывает, за сколько секунд маятник сделал одно полное колебание. А частота - сколько штук полных колебаний маятник сделал за 1 секунду. Частоту находим, если потребуется, как <<<Назад, к задаче А5 | Разбираем далее задачу А7 >>> |
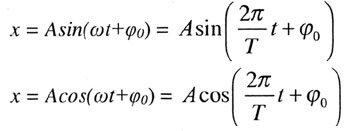
Там есть ещё один параметр 
. Это начальная фаза колебаний. Что такое вообще ФАЗА? Посмотрите на две верхние картинки - девочку на качелях и маятник. У них период не одинаковый. Поэтому бывают моменты, когда они качаются как бы синхронно, в одну сторону. В этом случае говорят, что их колебания совпадают по фазе. Но вот маятник начинает отставать по ФАЗЕ, отстаёт всё больше и больше, наступает даже такой случай, что они качаются в ПРОТИВОФАЗЕ. А в формуле нулевая фаза - это если маятник начал свои качания не из положения равновесия, а будучи отклонённым на какой-то угол. Этот угол и есть нулевая фаза. А ответ на задачку понятен - 