ДЕМОВАРИАНТ ЕГЭ ПО МАТЕМАТИКЕ 2015 ГОДА<<< Базовый уровень смотри здесьПрофильный уровеньСпецификация ЕГЭ по математике 2015 года (профильный уровень) посмотреть (скачать) здесь в PDF Кодификатор элементов содержания ЕГЭ по математике 2015 года посмотреть (скачать) здесь в PDF Демонстрационный вариант предназначен для того, чтобы дать представление о структуре будущих контрольных измерительных материалов, количестве заданий, их форме и уровне сложности. Задания демонстрационного варианта не отражают всех вопросов содержания, которые могут быть включены в контрольные измерительные материалы в 2015 году. Структура работы приведена в спецификации, а полный перечень вопросов — в кодификаторах элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения Вариант состоит из двух частей и содержит 21 задание. ЧАСТЬ 1Задание 1. Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути? Решение. Сутки - это 24 часа. Начало суток 0 - 00. Ночь. Время пошло: 1-00, 2-00, 3-00 итд. В 12-00 стрелки часов встали на то же место, что и в начале суток. Но - прошло только 12 часов, только половина суток. Потом 13-00, 14-00, 15-00 и так далее. Наконец, 22-00, 23-00, 23-57, 23-58, 23-59 и далее.... сколько? Можно сказать 24-00, а можно сказать 0-00 следующих суток. Простите, за такое дурацкое изложение, это, конечно, всем известно. Теперь о задаче. Поезд отправился в 23-50. Прошло всего 10 минут, как наступили следующие сутки. А в следующие сутки поезд был в пути 7 часов 50 минут. То есть, всего он был в пути 7-50 + 10 минут = 8 часов. Ответ 8 Задание 2. На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией.
Определите по рисунку, сколько месяцев из данного периода средняя температура была больше 18 градусов Цельсия. Решение. Достаточно мысленно провести горизонтальную линию по отметке 18 градусов. Само число 18 на оси температур не показано, но видно, что цена деления оси 2 градуса, то есть 18 будет посередине между 16 и 20. Мы видим, что четыре месяца 6; 7; 8 и 9 лежат выше этой линии. Обратите внимание: в условии сказано, что точки "для наглядности" соединены линией, сама по себе линия ничего не обозначает, числовое значение имет только точки. Ответ 4 Задание 3. Строительный подрядчик планирует купить 15 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице.
Во сколько рублей обойдётся наиболее дешёвый вариант покупки с учётом доставки? Решение. Эта задача на выбор оптимального варианта. Надо просто-напросто перебрать все варианты и выбрать лучший. Перебор тоже удобней делать в форме таблицы (хотя вовсе необязательно, можно и без таблицы) Сначала пересчитаем тонны в штуки. 15 000 / 5 = 3 000 штук. Подрядчик желает купить 3 000 штук кирпича
Как видно, самый дешёвый вариант покупки у поставщика Б, он составдяет 54 000 рублей, это число и следует записать в ответ. Ответ 54 000 Задание 4. Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки
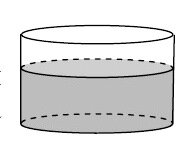
Решение. Ромб состоит из четырёх одинаковых треугольников с основанием 3 и высотой 2 сантиметра. Площадь треугольника равна половине произведения основания на высоту, (3х2)/2=3 Ответ 12 Задание 5. В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах. Решение. Делают некий ОПЫТ. Это термин такой в теории вероятностей. В нашей задачке опыт – вытягивание билета из сборника. У этого опыта возможно сколько-то ИСХОДОВ. В нашей задачке – возможно 25 исходов. P(A)= m / n В нашем случае m = 23, n= 25, P(A) = 23/25 = 0,92 Задание 6. Ответ и полное решение смотрите здесь Задание 7. Треугольник АВС вписан в окружность с центром О. Найдите угол ВОС, если угол ВАС равен 32 градуса. Ответ дайте в градусах. Решение. Эта задачка взята без изменения из ЕГЭ прошлого года. Подробный разбор этой задачки можно посмотреть ЗДЕСЬ. Ответ 64 Задание 8. На рисунке изображен график дифференциируемой функции.... И эта задачка полностью взята из ЕГЭ прошлого года, там она называлась В8. По ЭТОЙ ССЫЛКЕ переходите на страничку, где содержится её разбор. Ответ 3 Задание 9. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого? Ответ выразите в см.
Ответ и полное решение смотрите здесь ЧАСТЬ 2Задание 10. Найдите sinа , если cosа = 0,6 и п < а < 2п. Ответ и полное решение смотрите здесь Задание 11.
Ответ и полное решение смотрите здесь Задание 12 Ответ и полное решение смотрите здесь Задание 13. Весной катер идёт против течения реки в 1 и 2/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 и 1/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч). Задача из прошлогоднего ЕГЭ, полное решение смотрите ЗДЕСЬ. Задание 14.
Ответ и полное решение смотрите здесь Для решения задачки возможно, придётся, вспомнить производные, кое какая теория у нс есть ЗДЕСЬ Вот и всё. Остальные задания ЕГЭ с 15-го по 21-ое подробно решены в самом демонстрационном варианте ЕГЭ, нам нечего к этому добавить. Успехов! По этой ссылке можно скачать набор заданий базового варианта ЕГЭ 2015 для тренировки |